MATURITNÁ SKÚŠKA Z MATEMATIKY

Maturitná skúška z matematiky je dobrovoľná. Žiak môže dobrovoľne konať maturitnú skúšku aj z ďalších predmetov, ktoré sú súčasťou  učebných plánov študijného odboru, ktorý žiak študuje. Pod vykonaním dobrovoľnej skúšky sa rozumie aj absolvovanie len externej časti maturitnej skúšky alebo len internej časti maturitnej skúšky. V riadnom skúšobnom období môže žiak dobrovoľne konať maturitnú skúšku najviac z dvoch predmetov.
Ak žiak neuspel na maturitnej skúške z dobrovoľného predmetu maturitnej skúšky, táto skutočnosť nemá vplyv na úspešné vykonanie maturitnej skúšky a na vysvedčení o maturitnej skúške sa neuvádza.
Ak žiak nie je spokojný s výsledkom dobrovoľnej maturitnej skúšky, nemusí si dať známku na vysvedčenie o maturitnej skúške zapísať

CHARAKTERISTIKA ÚLOH MATURITNÝCH ZADANÍ

Úloha č. 1

Žiak objasní (definuje) dané pojmy, uvedie ich príklady a kontrapríklady, sformuluje ich vlastnosti a súvislosti medzi uvedenými pojmami (prevláda forma monológu).

Úloha č. 2

Úloha je zameraná na argumentáciu a dôvodenie (prevláda forma dialógu s členmi predmetovej maturitnej komisie).

Úloha č. 3

Úloha je zameraná na postup riešenia príslušnej úlohy s rôznymi alternatívami. Doplňujúce otázky budú zamerané na alternatívy pri iných číselných zadaniach.

Úlohy maturitných zadaní nemôžu byť z jedného tematického celku.

PREHĽAD ÚLOH  

Zadanie

Úloha č. 1

Úloha č. 2

Úloha č. 3

  1.  

Výroky

Vzájomná poloha 2 rovín

Vzťahy medzi hodnotami goniometrických funkcií
  1.  

Množiny

Závislosť povrchu a objemu kocky od telesovej uhlopriečky

Úpravy výrazov
  1.  

Postupnosti

Vzťahy medzi goniometrickými funkciami

Exponenciálne rovnice
  1.  

Aritmetická a geometrická postupnosť

Vzájomná poloha 2 priamok

Úpravy výrazov s faktoriálmi
  1.  

Logaritmus

Vlastnosti geometrickej postupnosti

Využitie Pytagorovej vety
  1.  

Odmocniny

Pravdivostná hodnota výroku

Využitie goniometrických funkcií v pravouhlom trojuholníku
  1.  

Analytické vyjadrenie priamok

Úpravy algerbraických výrazov

Rovnice s absolútnou hodnotou
  1.  

Intervaly

Goniometrické vzorce dvojnásobného uhla

Kombinácie
  1.  

Karteziánska sústava súradníc v rovine

Binomický rozvoj výrazu

Nerovnice
  1.  

Číselné množiny

Využitie vlastnosti kosoštvorca v analytickej geometrii

Využitie aritmetickej a geometrickej postupnosti
  1.  

Funkcie

Vlastnosti Pascalovho trojuholníka

Kružnica a šesťuholník
  1.  

Rovnice kružnice

Kombinačné čísla

Využitie aritmetickej postupnosti
  1.  

Kvadratická funkcia

Súčtové vzorce

Rovnice kružnice
  1.  

Vzájomné polohy 2 priamok, priamky a kružnice v stereometrii

Vlastnosti aritmetickej postupnosti

Definičné obory funkcií
  1.  

Algebraické výrazy

Vlastností exponenciálnej funkcie

Vzájomná poloha priamky a kružnice
  1.  

Mocniny

Vlastnosti kombinačných čísel

Povrch hranola
  1.  

Kvadratická rovnica

Monotónnosť postupnosti

Logaritmická rovnica

  1.  

Vzdialenosť 2 bodov, bodu od priamky a roviny v stereometrii

Iracionálna rovnica

Objem a povrch kvádra
  1.  

Exponenciálna funkcia

Trojuholník v analytickej geometrii

Aritmetická postupnosť v praxi
  1.  

Logaritmická funkcia

Geometrická postupnosť

Vlastnosti kvádra
  1.  

Sínusová a kosínusová veta

Trojuholník v analytickej geometrii

Objem valca
  1.  

Uhol 2 priamok, priamky a roviny v stereometrii

Iracionálna rovnica

Vzdialenosť bodov v rovine
  1.  

Rovinné útvary

Vzájomná poloha 2 priamok v rovine

Súradnice bodov v priestore
  1.  

Sústava súradníc v priestore

Binomický rozvoj výrazu

Vlastnosti pravouhlého trojuholníka
  1.  

Kruh, kružnica

Vzťahy medzi goniometrickými funkciami

Vlastnosti lichobežníka
  1.  

Lineárna funkcia

Aritmetická postupnosť

Kvadratické rovnice v slovných úlohách
  1.  

Kombinatorika

Korene kvadratickej rovnice

Určenie lineárnej funkcie
  1.  

Funkcia sínus

Vzájomná poloha priamky a kružnice

Kombinatorika
  1.  

Kombinačné čísla

Vlastnosti pravouhlého trojuholníka

Určenie kvadratickej funkcie
  1.  

Základné štatistické pojmy

Vlastnosti kombinačných čísel

Rovnice priamky v rovine

  Schválené pomôcky:  kalkulačka, tabuľky, modely telies

VZOROVÉ  ÚLOHY

1.       zadanie

–––––––––––––––––––––––––––––––––––––––––––––––––––––––-–––––  

Úloha č. 1
Definujte pojmy výrok, hypotéza, negácia výroku. Čo rozumieme pod pojmom pravdivostná hodnota výroku. Aké sú základné logické spojky a na čo sa používajú. Aké druhy zložených výrokov poznáte. Na konkrétnych príkladoch uveďte jednotlivé typy zložených výrokov.

Úloha č. 2
Dokážte, že roviny a: 2x – 5y + 4z – 10 = 0 a b: 4x - 10y + 8z -10 = 0 sú rovnobežné rôzne. Upravte predpis roviny tak, aby dané roviny boli       a) rovnobežné totožné                                                                                                                                          b) rôznobežné
Úloha č. 3
Bez určenia veľkosti uhla určte hodnoty ostatných goniometrických funkcií, ak:
,   

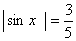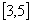
2.       zadanie

–––––––––––––––––––––––––––––––––––––––––––––––––––––––-––––  

Úloha č. 1  
Definujte kvadratickú funkciu. Vysvetlite ako súvisia vlastnosti kvadratickej funkcie.
f: y = ax2 + bx + c od hodnôt koeficientov a, b, c. Na grafe vysvetlite vlastnosti kvadratickej funkcie.  

Úloha č. 2
Odvoďte vzťah pre výpočet sin 2a, cos 2a pomocou vzťahov sin (a + b) a cos (a + b)

Úloha č. 3
Kružnica k je daná bodmi A 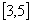 , B 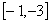. Sú to krajné body priemeru kružnice. Určte:

a)      súradnice stredu kružnice

b)      stredový a všeobecný tvar kružnice

c)   všeobecnú rovnicu priamky určenej bodmi AB

3.   zadanie

–––––––––––––––––––––––––––––––––––––––––––––––––––––––-–––––

Úloha č. 1
Vysvetlite sústavu súradníc v priestore, zvoľte si dva ľubovoľné body v priestore (pomocou súradníc), znázornite ich v súradnicovom systéme, vyjadrite vzťah pre výpočet ich vzdialenosti a súradnice stredu úsečky určenej týmito bodmi. 

Úloha č. 2
Pre akú hodnotu parametra aÎR sa prostredný člen binomického rozvoja výrazu 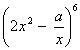rovná 1280x3 ?  

Úloha č. 3
V pravouhlom trojuholníku je rozdiel dĺžok odvesien 7 cm . Jeho obsah je 30 cm2. Vypočítajte dĺžku prepony.